
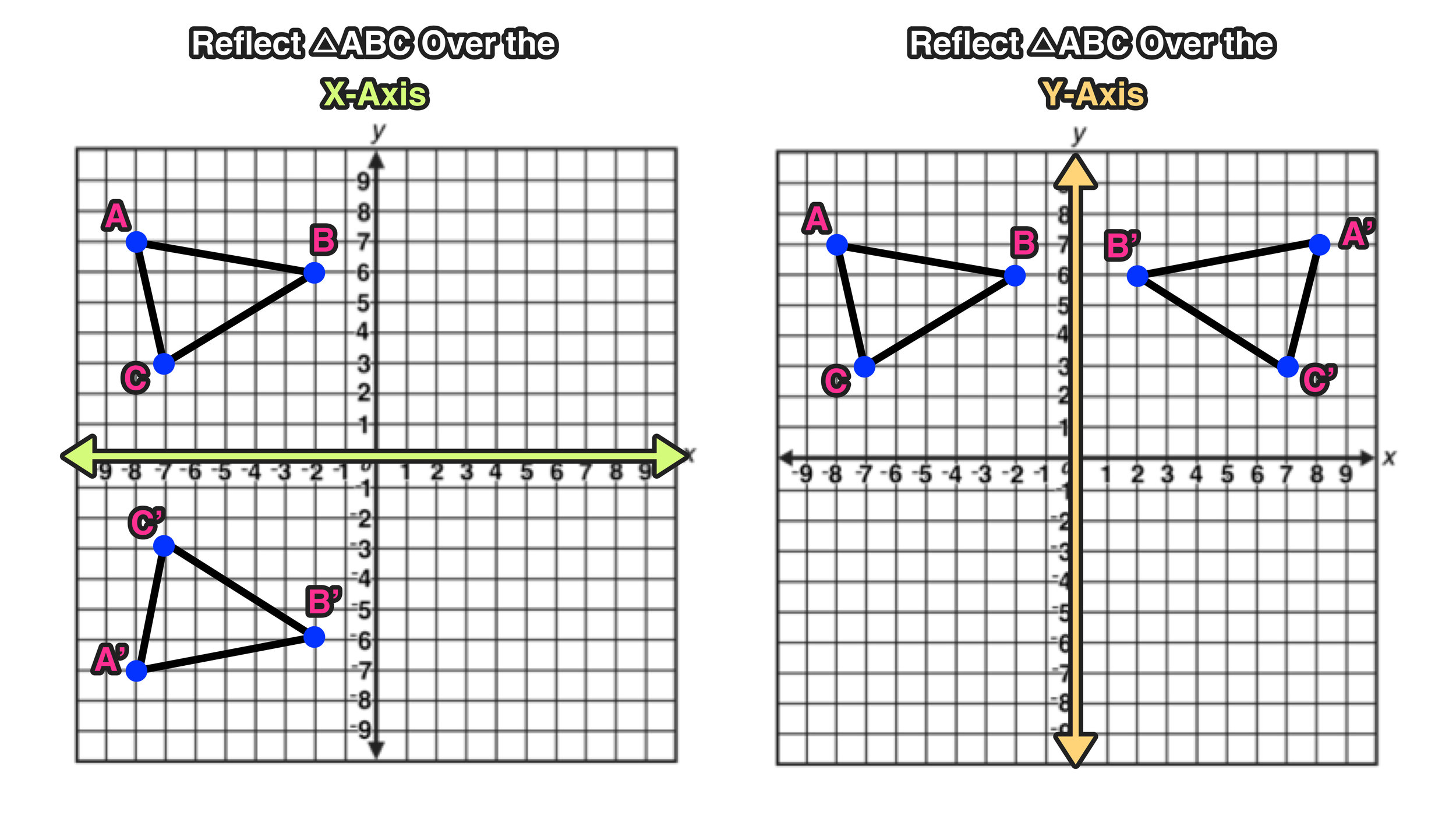
Here is an example: Reflect the graph vertically. Math Definition: Reflection Over the Y AxisĪ reflection of a point, a line, or a figure in the Y axis involved reflecting the image over the Y axis to create a mirror image. Another transformation that can be applied to a function is a reflection over the horizontal or vertical axis. A reflection over the x-axis can be seen in the picture below in which point A is reflected to its image A'. The x stays the same, and vice versa over the y axis. Example: (x, y) over the x axis is now (x, -y), If you come across the y already being a negative, then make it a positive, (x, -y) (x, y). In this case, the x axis would be called the axis of reflection. To reflect a point in the x axis, multiply it's y coordinate by -1.
#REFLECTION IN THE X AXIS HOW TO#
This complete guide to reflecting over the x axis and reflecting over the y axis will provide a step-by-step tutorial on how to perform these translations.įirst, let’s start with a reflection geometry definition: Math Definition: Reflection Over the X AxisĪ reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image. This idea of reflection correlating with a mirror image is similar in math. In real life, we think of a reflection as a mirror image, like when we look at own reflection in the mirror.

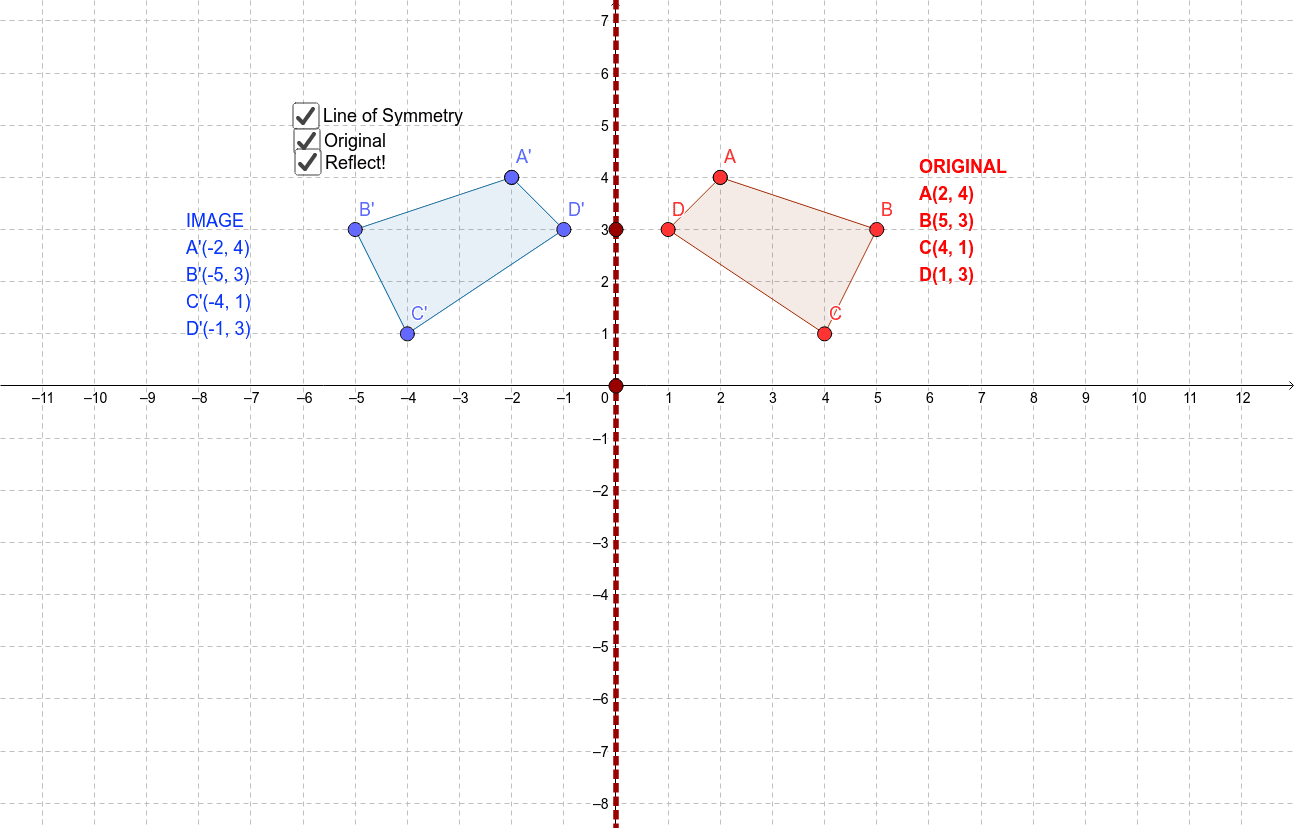
Learning how to perform a reflection of a point, a line, or a figure across the x axis or across the y axis is an important skill that every geometry math student must learn.


 0 kommentar(er)
0 kommentar(er)
